Conquer Fractions: Adding and Subtracting with Ease
Ever felt like fractions are a cryptic code you can't crack? Adding and subtracting them can seem daunting, especially when different denominators come into play. But fear not! When fractions share the same denominator, the process becomes remarkably straightforward. Let's unlock this mathematical mystery together.
Adding and subtracting fractions with common denominators is a foundational math skill that opens doors to more advanced concepts like algebra, geometry, and even everyday tasks like cooking and budgeting. Imagine slicing a pizza into equal parts and sharing it with friends. Fractions help us understand and quantify these portions with accuracy. Understanding this process also allows you to interpret data, percentages and proportions in a clearer, more informed manner.
The history of fractions dates back to ancient civilizations. Egyptians used unit fractions, which have a numerator of 1, while Babylonians preferred a sexagesimal system (base-60) for fractions, a system that influences how we measure time today. The concept of a fraction as we know it today – with both a numerator (top number) and denominator (bottom number) – was developed over centuries, with significant contributions from Indian and Arabic mathematicians. A clear understanding of fractional arithmetic became essential for trade, astronomy, and various scientific advancements.
One of the main issues students face when dealing with fraction operations is confusion arising from different denominators. However, when the denominators are the same, the process is significantly simplified. This makes the concept of adding and subtracting fractions with like denominators a crucial stepping stone to mastering fraction manipulation overall. It lays the groundwork for tackling more complex fraction calculations.
When adding or subtracting fractions with the same denominator, the denominator remains constant. Simply perform the required operation on the numerators. For example, if we want to add 3/5 and 1/5, we keep the denominator (5) and add the numerators (3 + 1 = 4). The result is 4/5. Similarly, subtracting 1/5 from 3/5 would be (3 - 1)/5 = 2/5.
Benefits of mastering this concept include: 1) Simplified calculations: Dealing with like denominators removes the complexity of finding a common denominator. 2) Foundation for complex fractions: This concept serves as a base for understanding more complex fraction operations, including those with unlike denominators. 3) Real-world applications: From splitting bills to adjusting recipes, understanding these fraction operations proves useful in everyday situations.
Action plan: 1. Identify if the denominators are the same. 2. Perform the operation (addition or subtraction) on the numerators. 3. Keep the denominator the same in the result.
Step-by-step guide: 1. Examine your fractions. Ensure the denominators are identical. 2. Add or subtract the numerators. 3. Write the result as a new fraction with the original denominator.
Advantages and Disadvantages of Adding/Subtracting Fractions with the Same Denominator
| Advantages | Disadvantages |
|---|---|
| Simplicity of calculations | Can be mistakenly applied to fractions with different denominators |
| Direct application of addition/subtraction rules | N/A |
Best Practice: Always double-check that the denominators are indeed the same before performing the operation. This helps avoid common errors.
Real World Examples: Sharing pizza slices (like denominators representing the total slices), combining portions of a recipe, calculating distances on a map with fractional miles.
FAQs: 1. What is a denominator? (The bottom number in a fraction representing the total parts of a whole). 2. Why do denominators need to be the same for addition/subtraction? (It's akin to adding apples and oranges; you need a common unit). And so on with other related FAQs.
Tips & Tricks: Visualize fractions using diagrams or real-world objects like pie slices to solidify your understanding.
In conclusion, mastering the art of adding and subtracting fractions with the same denominator is a fundamental skill that paves the way for more advanced mathematical concepts. From simplifying calculations to providing a foundation for complex fraction operations, this knowledge is essential for students and anyone working with numbers in daily life. By understanding the history, principles, and practical applications of these fraction operations, we empower ourselves to confidently tackle mathematical challenges and real-world problems. So embrace fractions, practice consistently, and unlock the potential of these mathematical tools to enhance your understanding of the world around you.
Y2k korean boy profile pictures a nostalgic trend
Tiny blood cells and pale hues decoding microcytosis and hypochromia
Score a sweet ride used cars and trucks in modesto

Adding And Subtracting Fractions With The Same Denominator W | Innovate Stamford Now
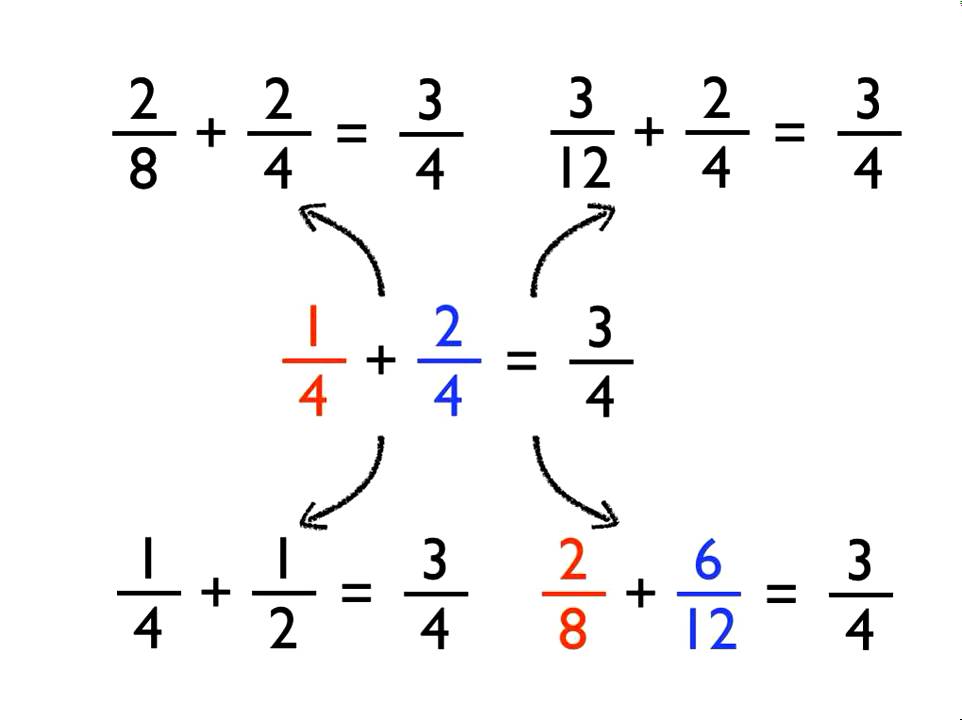
Subtracting Fractions With Different Denominators | Innovate Stamford Now

Subtracting Fractions Different Denominator Worksheet | Innovate Stamford Now

How to Add Fractions in 3 Easy Steps | Innovate Stamford Now
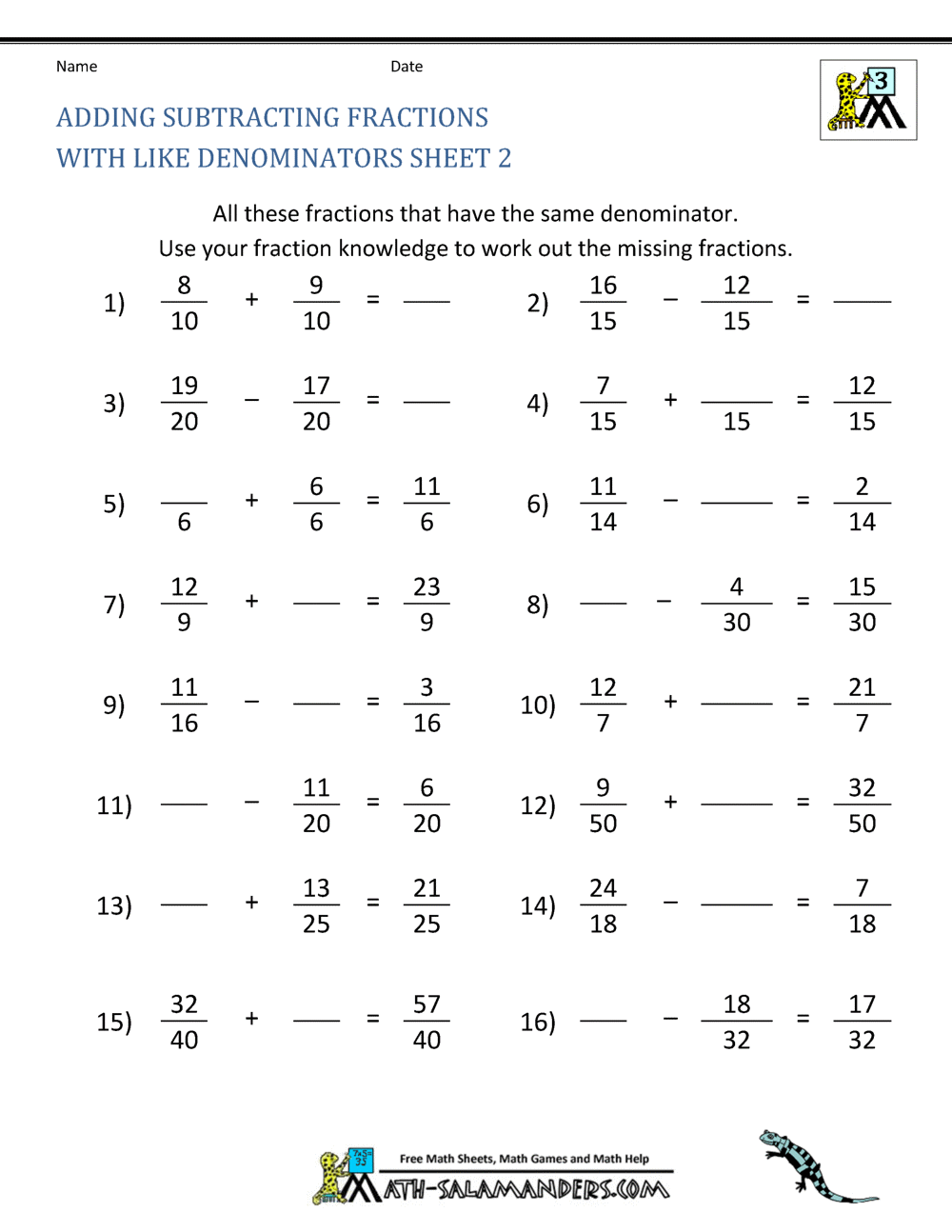
Worksheet On Addition And Subtraction Of Fractions | Innovate Stamford Now

Adding Subtracting Fractions With Unlike Denominators Worksheet | Innovate Stamford Now

How to Subtract Fractions in 3 Easy Steps | Innovate Stamford Now

Adding And Subtracting Fractions With Unlike Denominators Worksheet | Innovate Stamford Now

Free subtracting fractions with options to choose like or unlike | Innovate Stamford Now

Adding And Subtracting Like Fractions | Innovate Stamford Now

Scaffolded LCD Worksheet for AddingSubtracting Fractions w | Innovate Stamford Now

adding subtracting fractions same denominator | Innovate Stamford Now

Adding And Subtracting Fractions With Unlike Denominators Wo | Innovate Stamford Now

Add Fractions With Same Denominator Worksheet | Innovate Stamford Now

Adding Fractions With Unlike Denominators Worksheet | Innovate Stamford Now